Stephen J. Morgan

EMAT 6680

Assignment #8

Prompt:

Find the triangle of minimal perimeter that can be inscribed in a given triangle. For a start, you may want to restrict your investigation to the given triangle being acute.

Solution:

For this investigation let's look at it in two parts. First we will examine the case where the triangle is acute. However, after we do this we have to see if we can make the same assumptions about obtuse

triangles or not. So let's assume we have an arbitrary acute triangle, triangle ABC. From here let's make the orthotriangle within this triangle. To do this select a side of the triangle and it's opposite vertex.

a perpindicular line. We will want to procede to do this for all three sides of the triangle. After this is done,mark where the three perpindicular lines intersect within our original triangle, triangle ABC. Then

connect this points to form the inscribed triangle, triangle DEF. My claim is that this construction creates thetriangle with the minimal perimeter that can beinscribed in a given ACUTE triangle. It is

important to note this may not work for obtuse triangles! Click here to see a GSP construction.

From the GSP construction we can observe many things. It appears that this is the triangle of minimial perimeter that can be inscribed. However, for this to be true, we need to be able to manipulate the

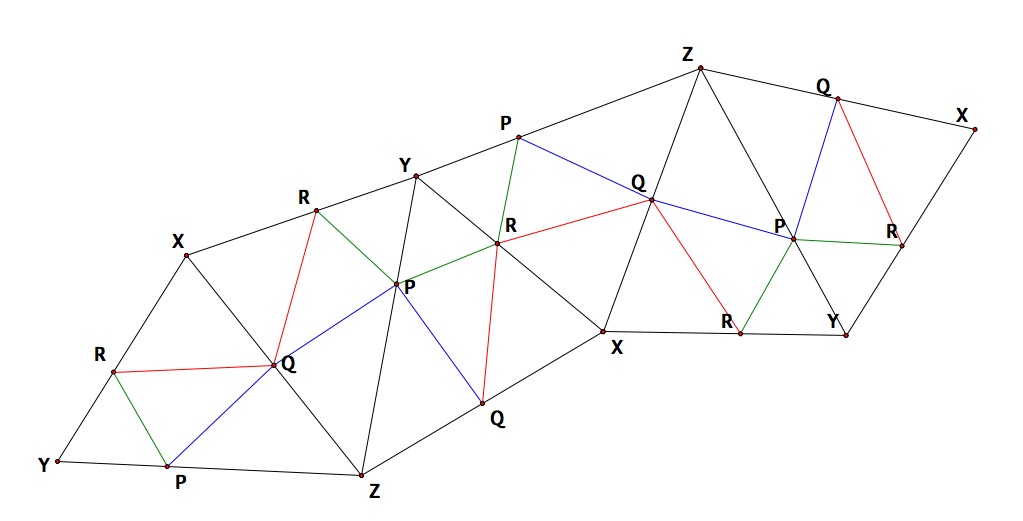
triangle, such that we can have all three sides of the inscribed triangle lie on the same line. This idea was used when H.A. Schwartz solved the problem, which was originally posted by Count Fagnano in 1775.

The gist of his proof is in the paragraph below. Refer to the picture below the proof for reference.

Picture of H.A. Schwartz's Proof:

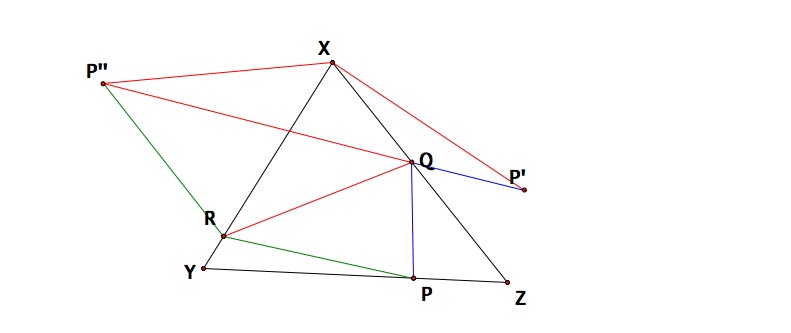
The problem was also solved another way by L. Fejer. His solution required reflecting a point P in XZ to obtain P' and P''. Then the perimeter of triangle PQR= P'Q+QR+RP". So for all inscribed triangles with

the fixed vertex P, the one whose vertices Q and R lie on the line P'P", has the minimum perimeter. We can easily see the triangle has the mirror properties at vertices Q and R. Therefore, for any position of

the point P on YZ there is a unique triangle of minimal perimeter. Its perimeter is given by P'P'' for some position of point P. Note that the angle P'X'P" equals twice the angle of X regardless of the position of

point P. Therefore, all triangles P'XP" are similiar. The triangle with the shortest base P'P" also has the shortest side XP'. But XP'=XP. Thus, there is a solution to Fagnano's problem and is where XP is

perpindicular to YZ. Using similiarity, YQ must be perpidicular to XZ and ZR to XY and we are done. Feel free to refer to the picture below.

Picture of L.Fejer's Proof

As far as obtuse triangles are concerned, the smallest perimeter of an inscribed triangle is not 1/2 the perimeter of the outer triangle. Additionally, there is no exact smallest perimeter. The perimeter of the inscribed triangle seems to be half of the outer

triangle's perimeter, but it is actually always slightly larger then this. It is converging towards 1/2 the perimeter of the outer triangle. However an inscribed triangle of perimeter 1/2 does not exist.